Over 50 million people filled out an NCAA March Madness bracket this year. Unfortunately, most of them will lose money. We know it’s almost impossible to fill out a perfect bracket (your odds are 1 in 9.2 quintillion). Even investing legend Warren Buffet will pay you $1mil a year for life if you can accomplish the feat. Yet, year after year, we all gather around office pools and social groups to attempt the impossible.
The reality is that you don’t need a ‘perfect’ bracket to win. You just need to beat your friends and family. At least, that’s what we tell ourselves subconsciously.
Still, if you’re like me (and millions of others), your bracket likely busted early in the tournament, and your investment is gone. The odds were always stacked against us from the start. Upsets of Kentucky, Auburn, North Carolina, Arizona, and cinderella teams like NC State and Alabama didn’t help either. With the Final Four now set to play this Saturday, our chances of winning are gone, and any hope of bragging rights (and money!) have disappeared.
This all got me thinking…
Was there a better way to invest that money in the last three weeks? And, even if I had won, was the juice worth the squeeze? What would be a better long-term bet: NCAA March Madness brackets or options trading?
Last month, we looked at Super Bowl odds to expose how difficult it is to find an edge in the sports betting market. We also recently talked to Jack Andrews from Unabated to hear how he approaches professional sports betting, quantitative edges, and using expected value (EV).
The goal of these blogs is not to say trading or betting is better than the other but to draw parallels and focus on the similarities that sports bettors can carry over into the options trading world and hopefully shine a light on how it’s easier to find +EV opportunities in options trading with more opportunities and consistency than in sports betting.
NCAA March Madness Bracket
Let’s use some simple math to highlight the odds and payout of a typical March Madness bracket.
Assume we entered a $100 March Madness pool. And let’s assume 20 people submitted a bracket. That gives us a 1 in 20 chance of profiting $1,900. That’s a 5% chance of a 1900% ROI. And a 95% probability of losing $100.
Low odds, high payout. It makes sense on the surface, but let’s dig deeper.
Approaching this from a statistical and probabilistic point of view, how many brackets (i.e., trades) does it take to be successful? We know that it takes approximately 1,000 trades to let probabilities play out. What would happen if we simulated these same bracket conditions over 1,000 occurrences?
A 5% assumed win rate gives us 50 wins and 950 losses, with a $1,900 profit on each winning bracket. This results in an Expected Value (EV) of zero.
EV = (50 x $1900) - (950 x -$100) = $0
The payout is proportional to the odds of success, which shouldn’t be surprising. Maybe slightly better odds than gambling against the casino in Vegas, but how do we find an edge if EV is $0?
There are probably better ways to invest that capital with a higher probability of positive expected value.
Use Trade Ideas to Find Positive EV
I went to Trade Ideas looking for a trade with $100 risk (similar to what I would have spent on a March Madness bracket) and much better probabilities of success. Of course, the reward/risk won’t be astronomical like the 1,900% a March Madness bracket returns in our example. But, over 1,000 trades, would it be a better bet?
I filtered for SPY trades with a 100%+ ROI, better than 50% of max profit, and positive EV:
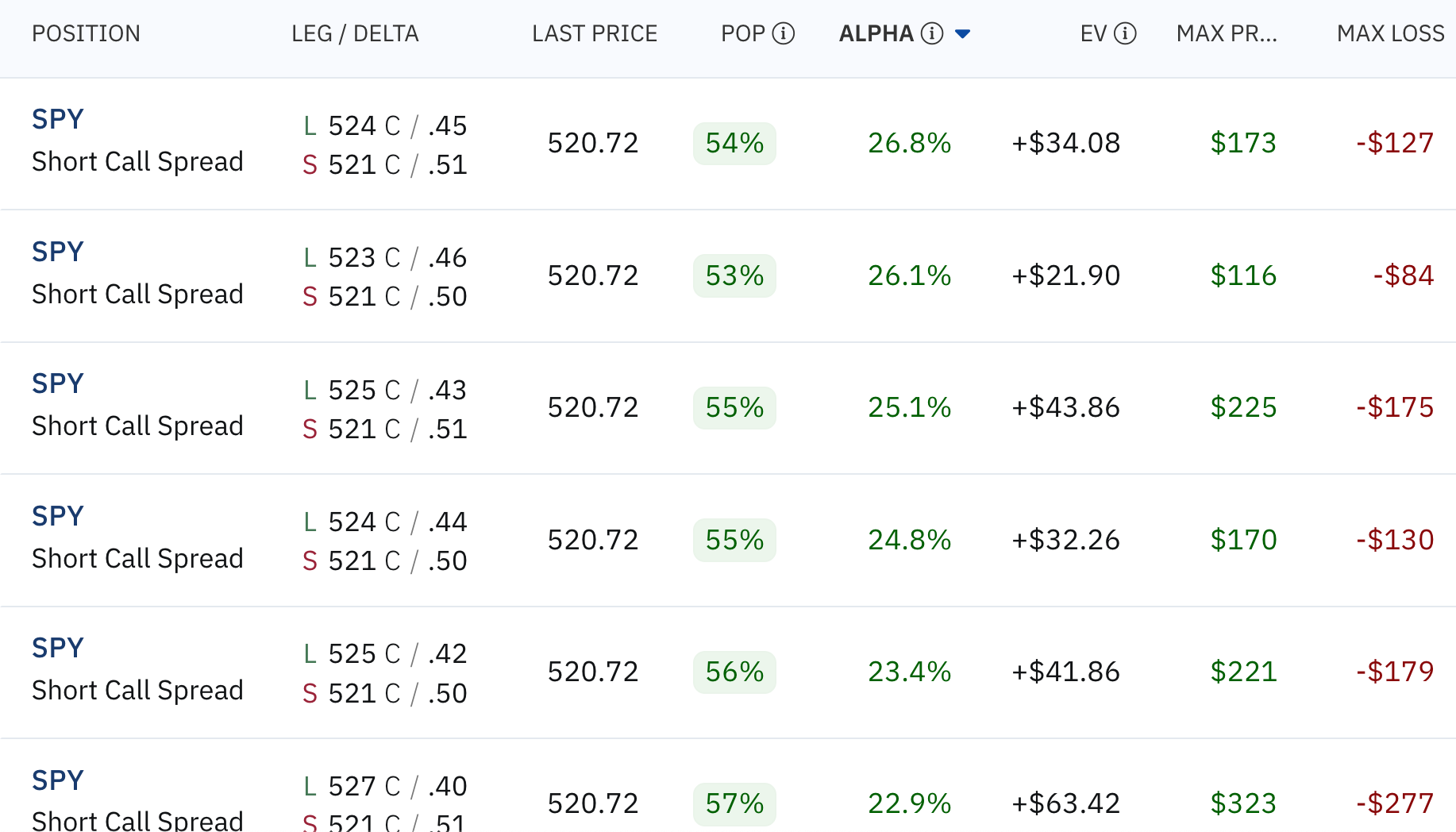
Let’s look at the second trade from the top more closely. Notice that I’m risking $100 to make $100, and I have a 51% chance of making $100 and a 41% probability of losing $100. That’s a no-brainer! It’s almost like flipping a weighted coin in my favor.
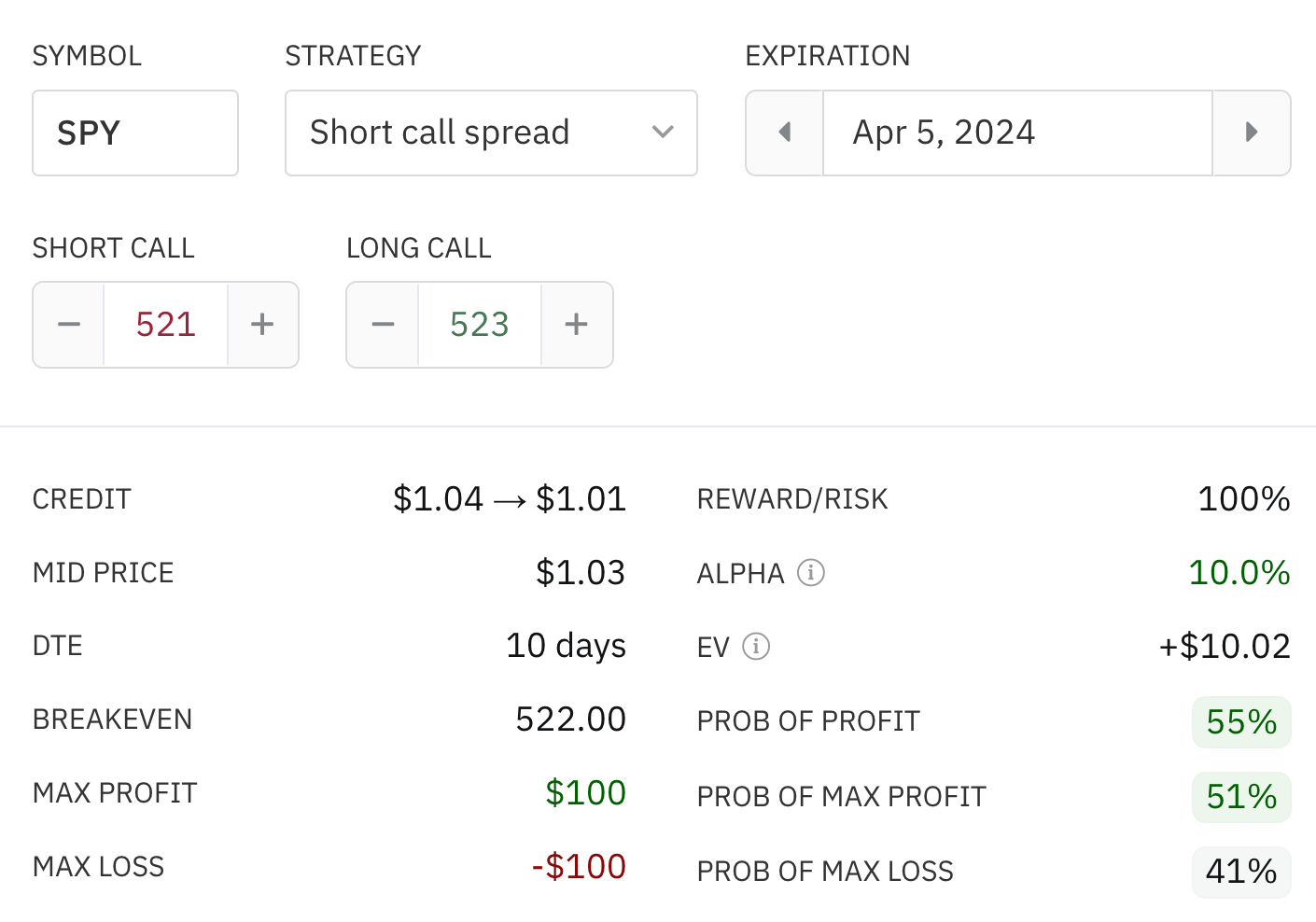
The expected value of this trade is +$10.02. Assuming 1,000 trades, that’s over $10,000. Incredible
It’s not easy, but with options trading, it’s possible to execute 1,000 trades. One trade per day gets us to 1,000 trades in four years, with $500 of new risk per week. If we tried to execute 1,000 “bracket” trades, we’d need to wait 1,000 years of NCAA tournaments to replicate the same law for large numbers of outcomes, which is impossible.
Hopefully, this will get all you casual sports bettors out there thinking about how to invest your capital using math and probabilities in your favor, as opposed to chasing the big lottery ticket. I’m the first to admit I’ll be right here again next year, eager to fill out another (probably losing) bracket, hoping to win some money and bragging rights - but I realize it’s more for fun than profit. Until then, I’ll be making hundreds of data-driven intelligent trades using options.

.png)









