Max pain is the strike price at which the maximum number of options would expire worthless for a given expiration. This price has the most open call and put option contracts for a symbol’s expiration date, and, theoretically, should the stock close at this price on expiration, most option traders would lose money. This is why it’s often referred to as the “max pain” in options trading.
We can visualize any symbol’s max pain and the notional value of all calls and puts for each strike price and expiration date. The $ value in each bar represents the total value of all outstanding options if the stock price closes at that strike price at expiration. The lower the value, the more "pain" for options traders.
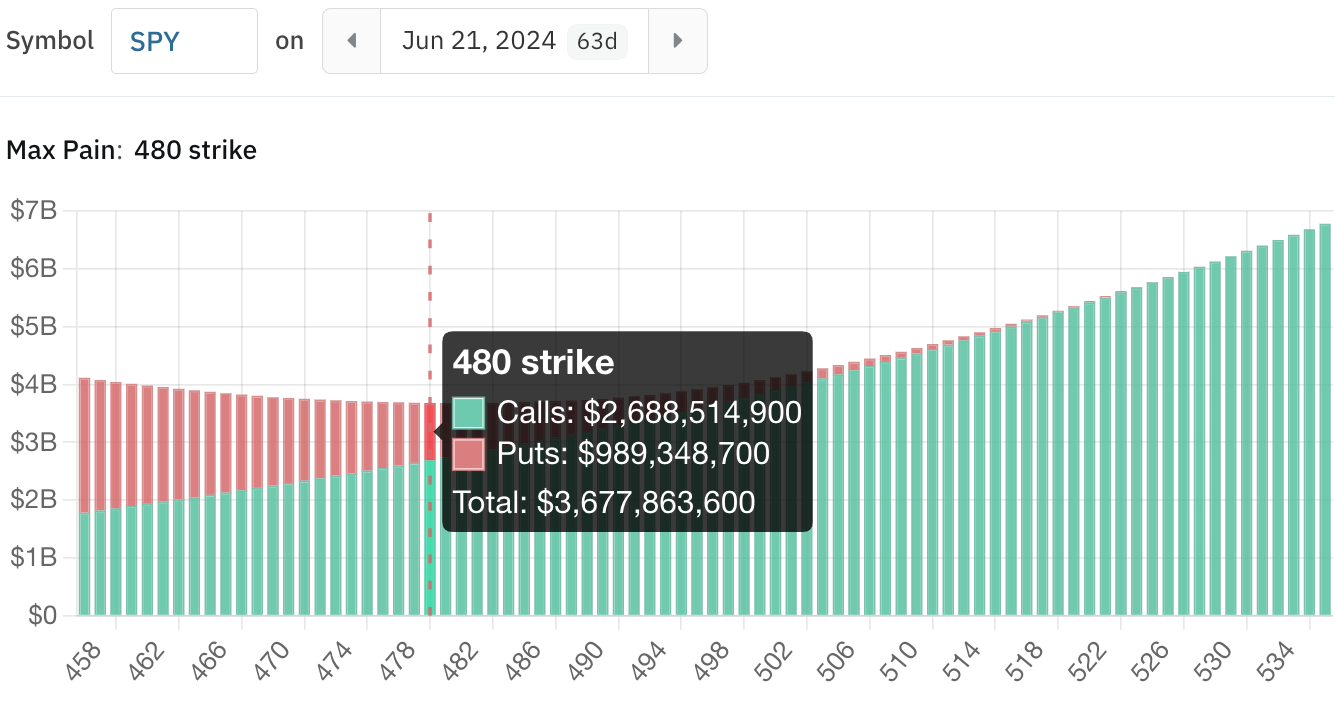
For example, the max pain for SPY’s June 21st expiration is the 480 strike. If SPY closes at 480 on that date, more than $3 billion in option contracts would expire out-of-the-money.
How to Calculate Max Pain
We can calculate max pain using the open interest for each strike price. Simply add the value of all open call and put contracts for a specific expiration, and the strike price with the highest cumulative value of open contracts is the max pain strike.
Max Pain Calculation:
- Calculate the intrinsic value for in-the-money calls and puts
- Multiply each contract’s intrinsic value by its open interest
- Add the call and put values together for each strike price
- The strike price with the highest value is the max pain point for that expiration
Below is the open interest for SPY’s 480 strike price, expiring June 21st.

Max Pain Theory
The Max Pain theory suggests that a stock’s price will tend to approach the strike price at which the largest number of options (both calls and puts) would expire worthless, aka the max pain price, as it nears expiration. The "pain,” therefore, is felt by option buyers who lose the entire value of their options, while option sellers benefit as the contracts expire out-of-the-money and they keep the credit received from selling the options.
The theory assumes that option writers, typically large institutions or professional traders, have the resources and market influence to drive the stock’s closing price toward the max pain point on expiration day. This suggests that market makers who write the options will hedge their positions to maintain a delta neutral portfolio. As their positions approach expiration, the market makers will offset their short option positions by selling or buying the contract’s underlying stock, therefore influencing the price toward the max pain point.
Using Max Pain in Options Trading
If we believe the max pain theory, it can help identify areas of potential support and resistance, especially as options expiration approaches, using the assumption that price will drift toward the max pain point. However, the max pain price changes constantly because the market is not static, so it is difficult to use an options strategy solely focused on max pain alone.
Max Pain Example
Suppose you have an expiration with the following strike prices and open interest:
- $102 OI = 200 contracts, OI = 100 contracts
- $101C OI = 300 contracts, $101P OI = 200 contracts
- $100C OI = 1000 contracts, $100P OI = 1000 contracts
- $99C OI = 400 contracts, $99P OI = 1000 contracts
- $98C OI = 300 contracts; $98P P OI = 500 contracts
If the underlying closes at $101 at expiration, the total value of all the options listed above:
$102 = (200 x 0) + (100 x $1) = $100 x 100
$101 = (300 x 0) + (200 x 0) = 0
$100 = (1000 x $1) + (1000 x 0) = $1000 x 100
$99 = (400 x $2) + (1000 x 0) = $800 x 100
$98 = (300 x $3) + (500 x 0) = $900 x 100
Total = $2,800 x 100 = $280,000
If the underlying closes at $100 at expiration, the total value of all the options listed above:
$102 = (200 x 0) + (100 x $2) = $200 x 100
$101 = (300 x 0) + (200 x $1) = $200 x 100
$100 = (1000 x 0) + (1000 x 0) = 0
$99 = (400 x $1) + (1000 x 0) = $400 x 100
$98 = (300 x $2) + (500 x 0) = $600 x 100
Total = $1,400 x 100 = $140,000
If the underlying closes at $99 at expiration, the total value of all the options listed above:
$102 = (200 x 0) + (100 x $3) = $300 x 100
$101 = (300 x 0) + (200 x $2) = $400 x 100
$100 = (1000 x 0) + (1000 x $1) = $1000 x 100
$99 = (400 x 0) + (1000 x 0) = 0
$98 = (300 x $1) + (500 x 0) = $300 x 100
Total = $2,000 x 100 = $200,000
In this example, the max pain point would be the $100 strike since it results in the lowest total intrinsic value for all options at expiration ($140,000).







