The options Greeks are used to measure the sensitivity of an option’s price to changes in underlying variables. Options traders can use the Greeks as a tool to understand how various factors such as implied volatility and time decay impact a position's value.

What are the 5 option greeks?

The five main option greeks are Delta, Gamma, Theta, Vega and Rho. 

• Delta measures the rate of change in an option’s price relative to a one-point move in the underlying asset. 
• Gamma measures the rate of change in delta per one-point move in the underlying asset. 
• Theta measures how much time decay affects an option’s value over a one day period. 
• Vega measures how much volatility affects an option’s value. 
• Rho measures how much interest rates affect an option’s value.

Delta and gamma are dependent on the option’s strike price relative to the underlying asset’s price and are therefore derived from intrinsic value. Theta, vega, and rho are determined by time to expiration, volatility, and interest rates, all of which are components of extrinsic value. Vega is an unknown variable, as implied volatility is forward looking and can’t be predicted. Interest rates typically impact longer-dated options more.

Delta 

Delta is the amount an options price should change based on a $1 move up in the stock. 

Call options have a positive delta between 0 and 1, while puts have a negative delta between 0 and -1.

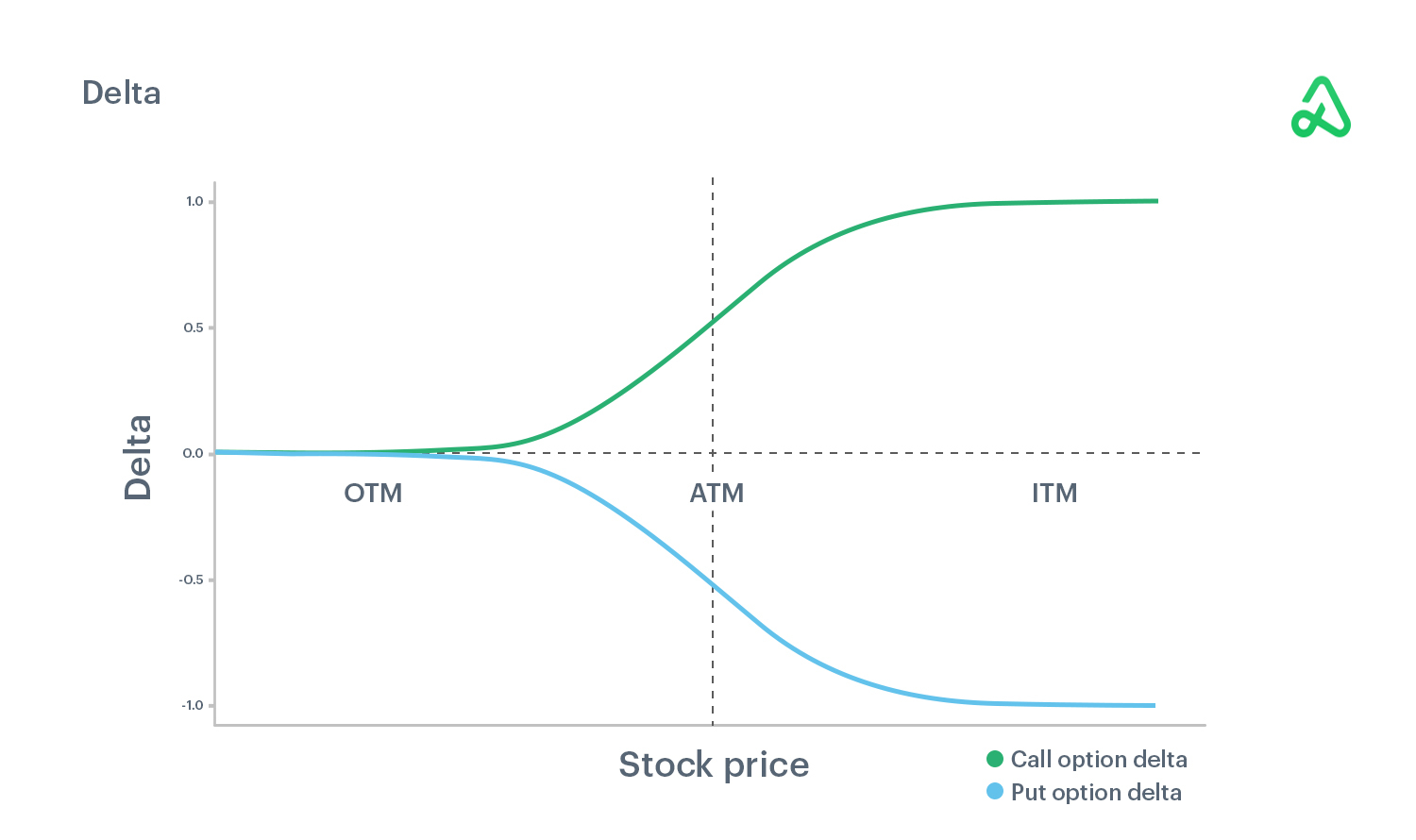
Delta can also be used to represent the number of relative shares you would own if you purchased an option at a specific delta. Buying a call option with a 0.30 delta is roughly equivalent to owning 30 shares of stock.

Delta can also act as an approximation of the probability an option will finish in-the-money. A 0.50 delta has roughly a 50% chance of expiring in-the-money.

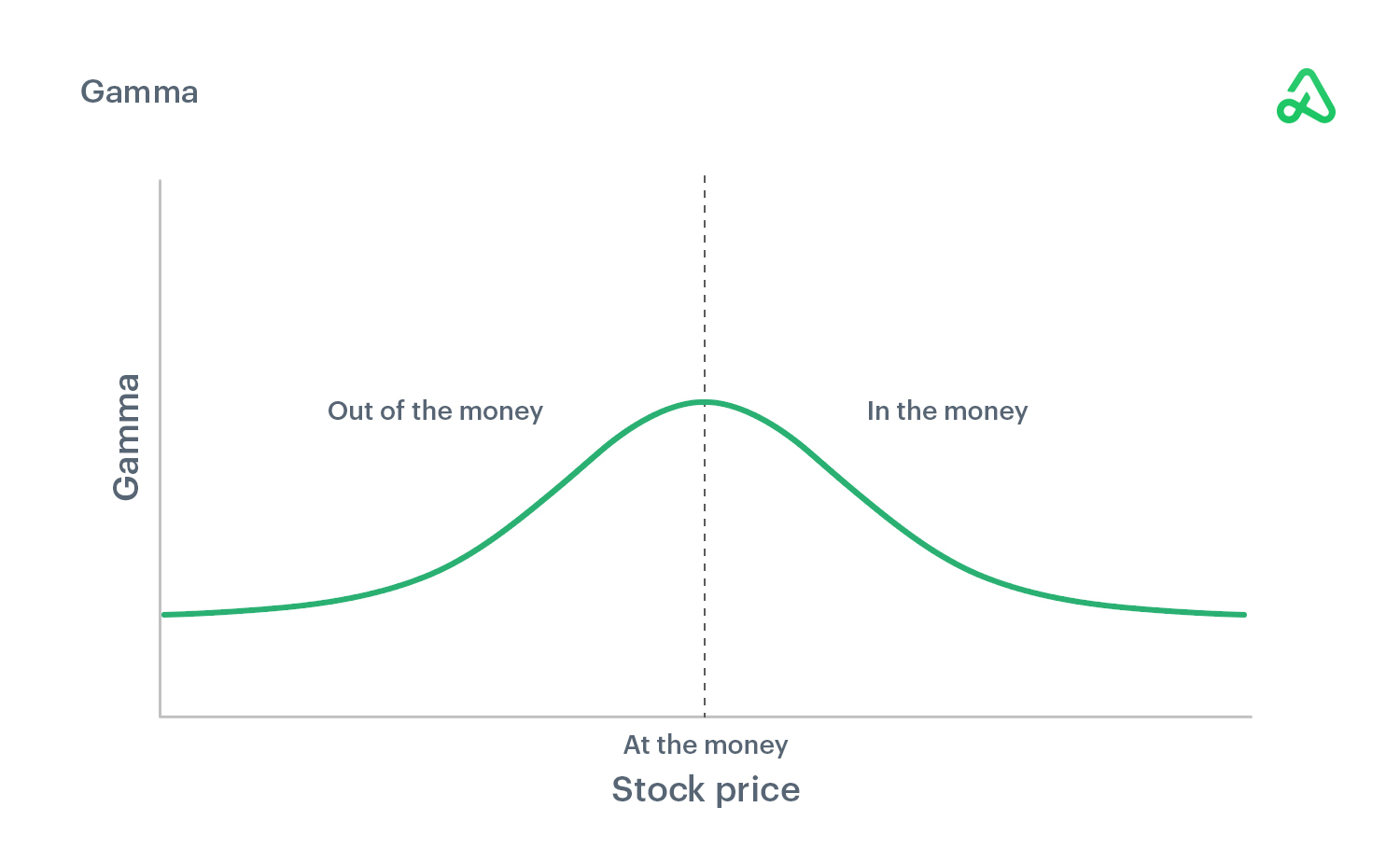
Gamma 

Gamma is the rate of change in delta for every $1 change in the underlying price. Gamma represents the acceleration at which an option's price increases or decreases. Think of gamma as the next dollar move.

For example, if an option has a delta of 0.60 and a gamma of 0.10, the first dollar move in the underlying asset will see the price of the option change by $0.60. The subsequent dollar move of the stock will see the price of the option change another $0.60 ($40) plus an additional $0.10 because of gamma.

Gamma is highest for contracts closer to at-the-money and declines as an option moves farther in-the-money or out-of-the-money.

Theta 

Theta is the effect time decay has on the value of an option. Options are a decaying asset and lose value every day, no matter what. Because of this, Theta is an advantage for the option seller and a disadvantage for the option buyer.

Theta is smaller on long-dated options but time decay accelerates as expiration approaches. The rate at which options contracts lose value increases exponentially.

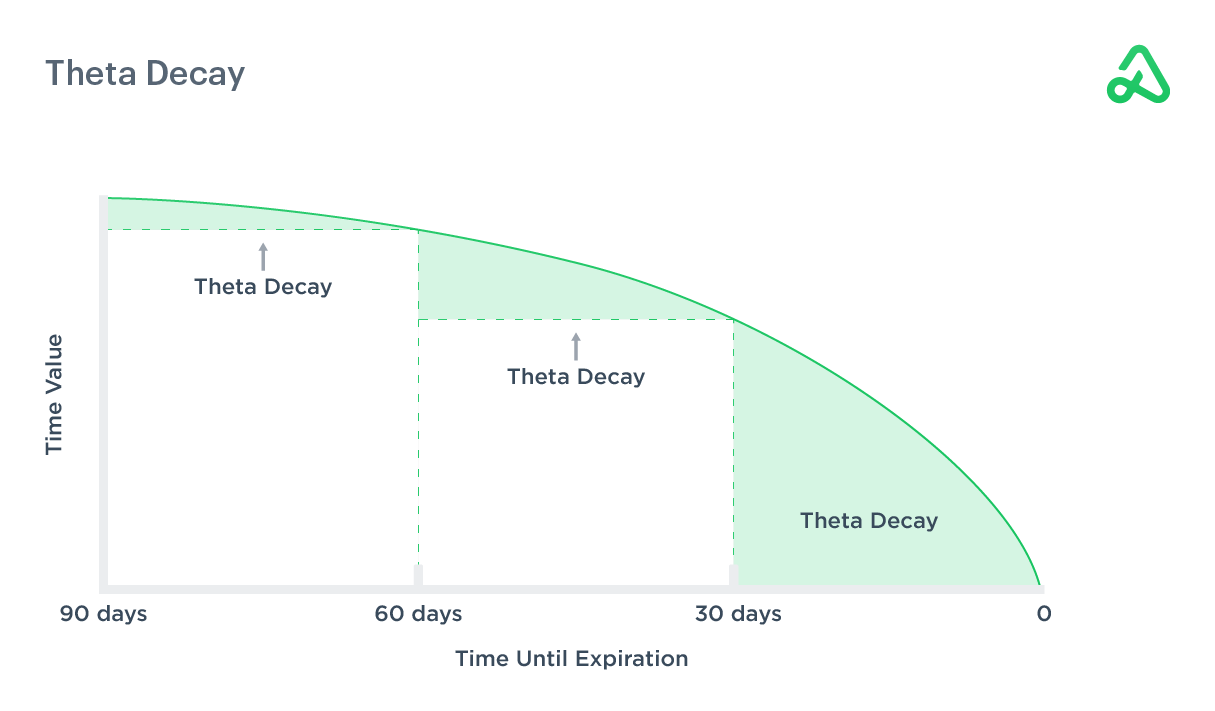
Theta is the amount the price of the option will decrease each day and is always represented as a negative value. For example, a theta value of -.04 means the option will lose $0.04 each day.

Vega 

Vega is the amount an option’s value changes for a 1% change in implied volatility in the underlying security. As volatility increases, an option’s price goes up as market participants anticipate an above-average move may be coming. Vega declines as an option approaches expiration because there is less time for volatility to impact the option’s value.

Unlike the other components of an option’s price (spot price, strike price, and time to expiration), Vega is an unknown element because future volatility can’t be predicted or forecasted. Therefore, Vega does not impact the intrinsic value because it is not based on the stock’s changing price, only changes in volatility.

Rho

Rho measures an option’s sensitivity to changes in interest rates. Rho represents the expected change of a contract’s value for a 1% change in interest rates. Rho is not as important for short-term options traders because changes in interest rates are usually relatively small, and only adjusted once per quarter, if at all.

Long-term options, or LEAPS, can be impacted by changes in interest rates because of their long expiration period and future uncertainty.