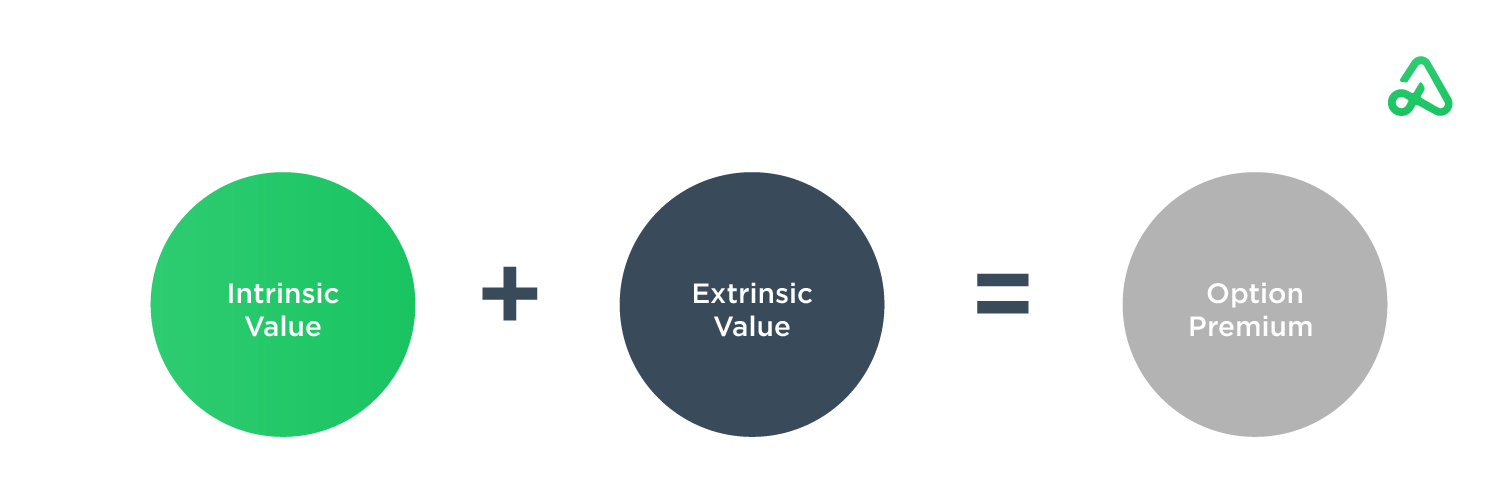
An option’s price, or value, is determined by the price of the option’s underlying asset and the terms of the options contract. The price of an options contract is also called the option premium.

The underlying security's price, the option's strike price, the time remaining until expiration, the the underlying security's volatility, the current risk-free interest rate, and the dividend rate of the underlying security are all considered in determining an option contract's price.

Intrinsic value

The intrinsic value of an options contract is the value of the option at expiration. If the contract expired immediately, the intrinsic value would be the only value remaining on the contract.

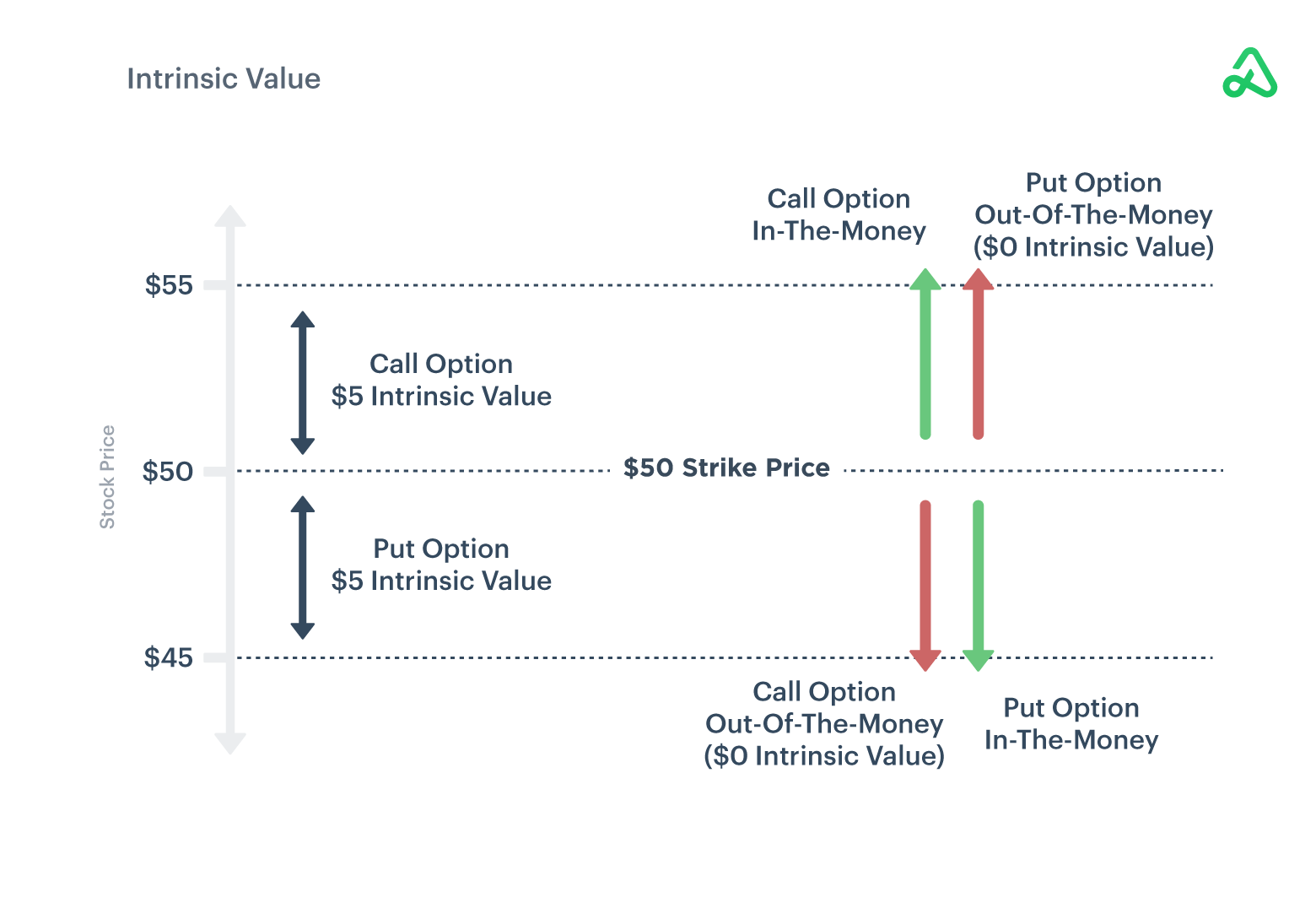
To calculate the intrinsic value, take the difference between the current price of the underlying security and the option contract’s strike price. The underlying security’s current price, above or below the option contract’s strike price, is the amount the contract is in-the-money.

A call option contract’s intrinsic value is the amount the underlying’s current price is above the strike price.

For example, if stock XYZ is trading at $55 per share, a call option with a $50 strike price would be in-the-money and have an intrinsic value of $5. If the underlying security’s price is below the call option’s strike price, the call option is out-of-the-money and the intrinsic value would be $0.

Likewise, the intrinsic value of a put option contract is the amount the underlying’s current price is below the strike price.

For example, if stock XYZ is trading at $45 per share, a put option with a $50 strike price would be in-the-money and have an intrinsic value of $5. If the underlying security’s price is above the put option’s strike price, the put option is out-of-the-money and the intrinsic value would be $0.

In most cases, the options contract’s value will exceed the intrinsic value because of external factors like time until expiration and volatility. The excess value beyond the intrinsic value is referred to as extrinsic value.

Intrinsic value is dependent on the strike price of the options contract. All else being equal, as the strike price increases, the value of a call option decreases, and the value of a put option increases. In this example, as the strike price increases, the put option’s value increases because the underlying security can be put to an option seller at a higher price.

Moneyness

Moneyness is used to describe the amount of intrinsic value for an options contract. Moneyness is described in three categories: in-the-money, at-the-money, and out-of-the-money. The degree of moneyness can change over the life of an options contract.  

In-the-money (ITM)

In-the-money options contracts are contracts with positive intrinsic value. For example, a call option is in-the-money if the underlying security’s price is higher than the option contract’s strike price.

A call option with a $50 strike price is in-the-money if the underlying security’s current price is above $50.

At-the-money (ATM)

At-the-money options contracts are contracts where the option’s strike price is equal to the underlying’s current price. A call option with a $50 strike price is at-the-money if the underlying security’s current price is $50.

At-the-money options contracts have the greatest extrinsic or time value because of the potential for changes in intrinsic value. 

Out-of-the-money (OTM)

Out-of-the-money options contracts have no intrinsic value because the contracts are “out-of-the-money” to be exercised based on the current underlying security’s price and the contract’s strike price. For an out-of-the-money call option, the underlying price is less than the option’s strike price.

Exercising an out-of-the-money options contract does not result in a positive payoff. A call option with a $50 strike price is out-of-the-money if the underlying security’s current price is below $50.

Deep-in-the-money (DITM)

Deep-in-the-money options contracts have a strike price significantly in-the-money. For a call option, the options contract’s strike price would need to be significantly below the current price of the underlying security. For a put option, the strike price would need to be significantly above the current price of the underlying security.

Generally, options contracts that are more than $10 in-the-money are considered deep-in-the-money. Deep-in-the-money options have significant intrinsic value and the other components of options pricing--such as time, volatility, etc.--have less of an impact on the option’s value. 

Deep-out-of-the-money (DOTM)

Deep-out-of-the-money options contracts have a strike price significantly out-of-the-money. Because out-of-the-money contracts have no intrinsic value, the value of deep-out-of-the-money options contracts comes from time, volatility, and other options pricing components.

For deep out-of-the-money options contracts to have value at expiration, the underlying security’s price will have to approach and then exceed the options contract’s strike price. Therefore, the value of a deep-out-of-the-money contract is dependent on a relatively large move in the underlying security.

Extrinsic value

Extrinsic value is the value of an options contract beyond its intrinsic value. The extrinsic value of an options contract is also called the time value because the remaining value is dependent on external factors such as the time remaining on the contract, the volatility of the underlying security, the current risk-free interest rate, and the dividend rate of the underlying security.

If the price of the underlying security is far above or far below the contract’s strike price, then the extrinsic value factors have little influence on the option’s price.

Extrinsic value is greatest when an options contract is at-the-money. Extrinsic value decreases as options contracts get deeper in-the-money or deeper out-of-the-money or closer to expiration.

Extrinsic value can be viewed as the true cost of an options contract because the extrinsic value represents the cost of the opportunity to benefit from future price movements of the underlying security. 

Time value

Time value is the difference between the options contract’s price and the intrinsic value of the option. As the time remaining until expiration decreases, the time value of the options contract also decreases. The longer the time until the options contract expires, the greater the opportunity for the underlying security’s price to move and increase its intrinsic value.

Before expiration, the time value of an option is at least 0 and is almost always positive.

Time value decay refers to the decline in the value of an options contract as it approaches expiration. Time decay is non-linear, meaning the rate of change increases as the options contract approaches expiration.

The rate of time decay for an options contract is called theta. Time decay, theta burn, and theta decay are synonymous.

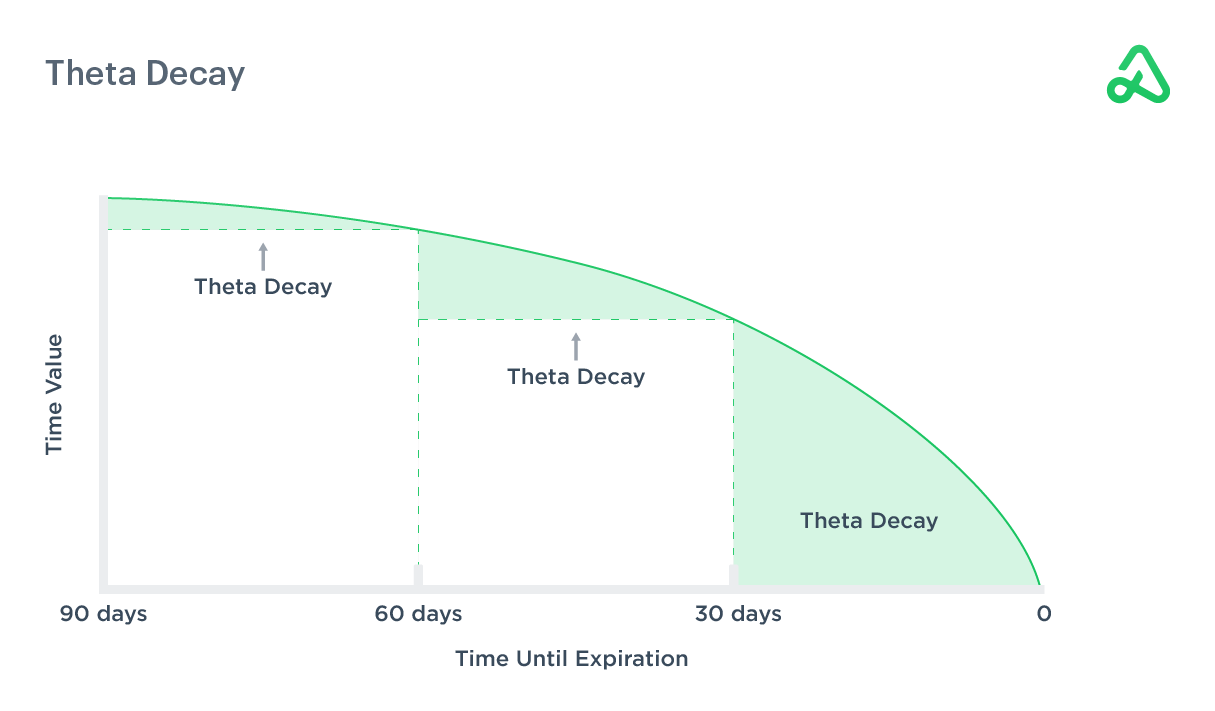
The image above illustrates how the time value of an options contract decreases at an accelerating rate as expiration approaches. Time decay increases more rapidly from 60 to 30 days than from 90 to 60 days, for example.

While an option’s time value decreases as expiration approaches, other extrinsic factors, such as Gamma and Vega, may increase as expiration approaches, offsetting or exceeding Theta decay.

Volatility

Volatility in options contracts refers to the fluctuation in the price of the underlying security. Volatility represents the likelihood of the underlying security moves up or down. Securities with stable prices have low volatility, while securities with large and frequent price movements have high volatility.

Volatility is an important determinant of an option’s price. Intrinsic value, the time remaining until expiration, and the volatility of the underlying security are the three primary factors contributing to an option’s price. The greater the volatility of the underlying security, the higher the premium of the options contract.

With increased price volatility, the range of possible payoffs is larger for the options contract. Higher implied volatility indicates a higher expectation for change in the options contract’s price value. The volatility of an options contract is called Sigma. 

Historical volatility

Historical volatility, or statistical volatility, is backward-looking and describes the price movement of an underlying security in the past. Historical volatility is typically presented for a specified range, such as the previous 20 days or over the past year.

When presented graphically, historical volatility, whether increasing or decreasing, displays the level of uncertainty in price movements for the underlying security. While the standard “past performance is not indicative of future returns” holds true, historical volatility gives context to the security’s implied volatility.

Implied volatility

Implied volatility is forward-looking and represents the amount of volatility expected in the future.

When calculated, implied volatility represents the expected one standard deviation move for a security.

Implied volatility increases with large price movements in the underlying security. As implied volatility rises, an options contract’s price increases because the expected price range of the underlying security increases.

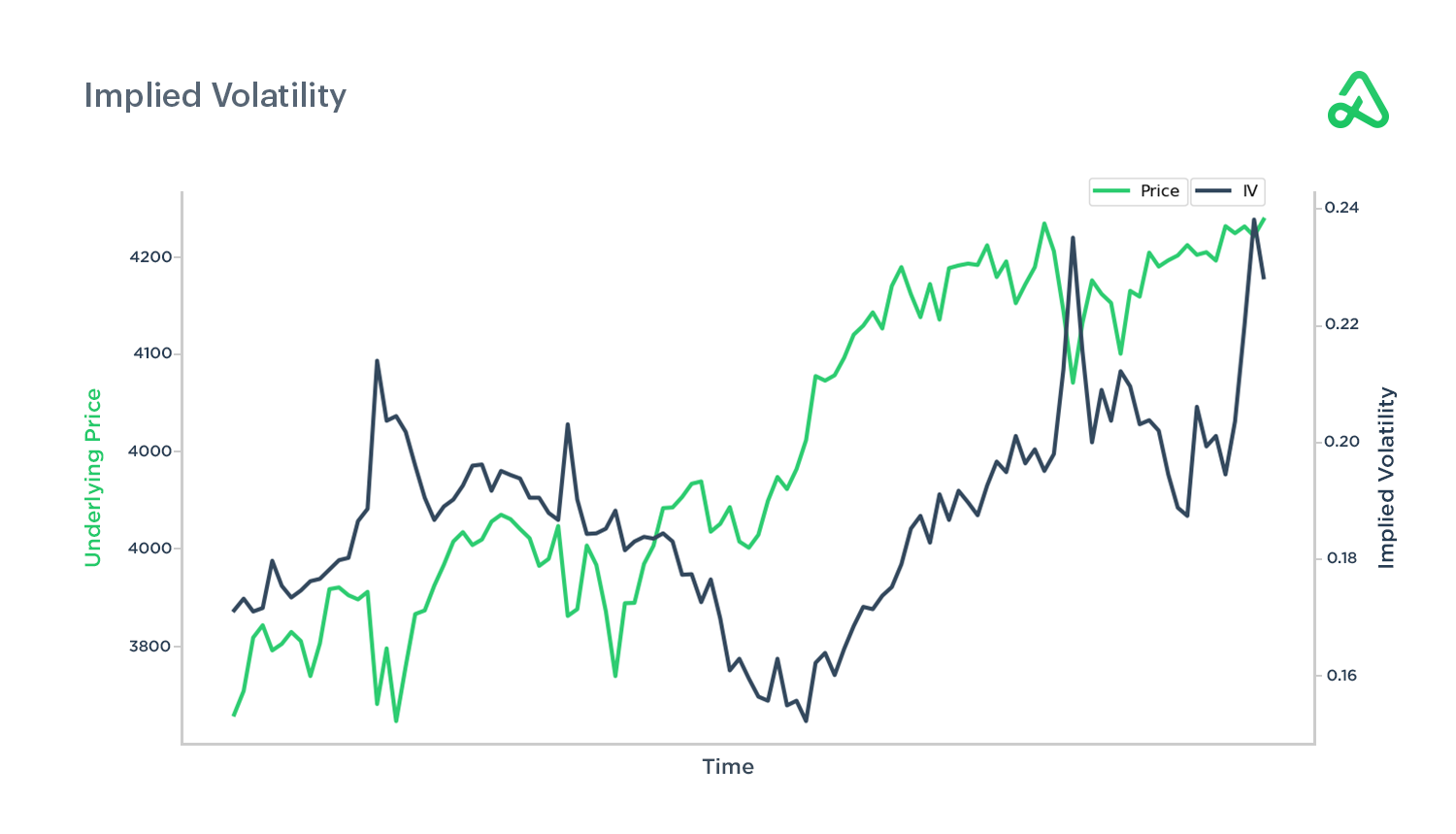
Implied volatility tends to increase, known as implied volatility expansion, before events such as earnings releases or important Federal Reserve announcements because these types of events bring uncertainty to the market. Implied volatility decreases after the event--known as implied volatility contraction--when the uncertainty is removed.

Implied volatility tends to be overstated relative to actual or historical volatility. 

IV rank

Implied volatility (IV) rank calculates where current implied volatility is compared to values over the past year. Implied volatility is an absolute value, so IV rank puts that absolute value into context by stating the current IV compared to the one year high and low.

For example, if a security had implied volatility between 20 and 40 over the past year and the current reading is 30, then the IV rank for the security would be 50 because IV is at the midpoint of the past year’s range.

IV percentile

Implied volatility (IV) percentile represents the current implied volatility relative to past values. IV percentile is similar to IV rank, but IV percentile describes the percentage of days over the past year that implied volatility was below the current level.

For example, an IV percentile of 90 means that implied volatility was below the current level 90% of the time the past year.

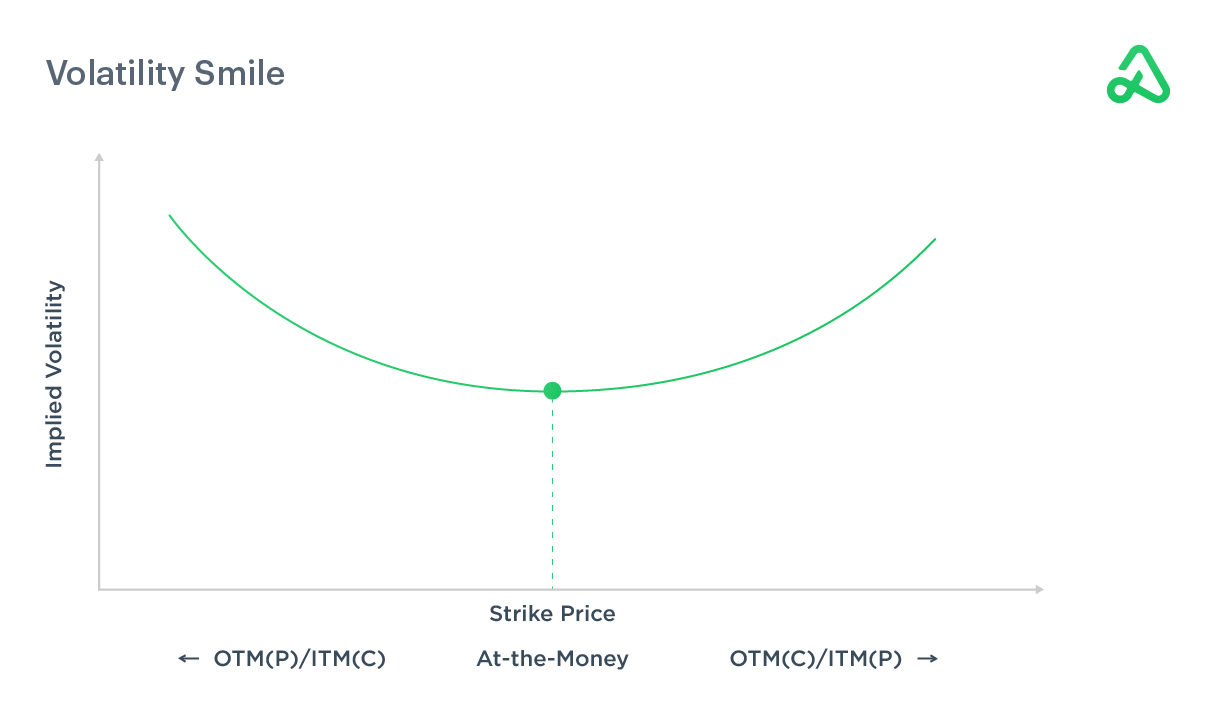
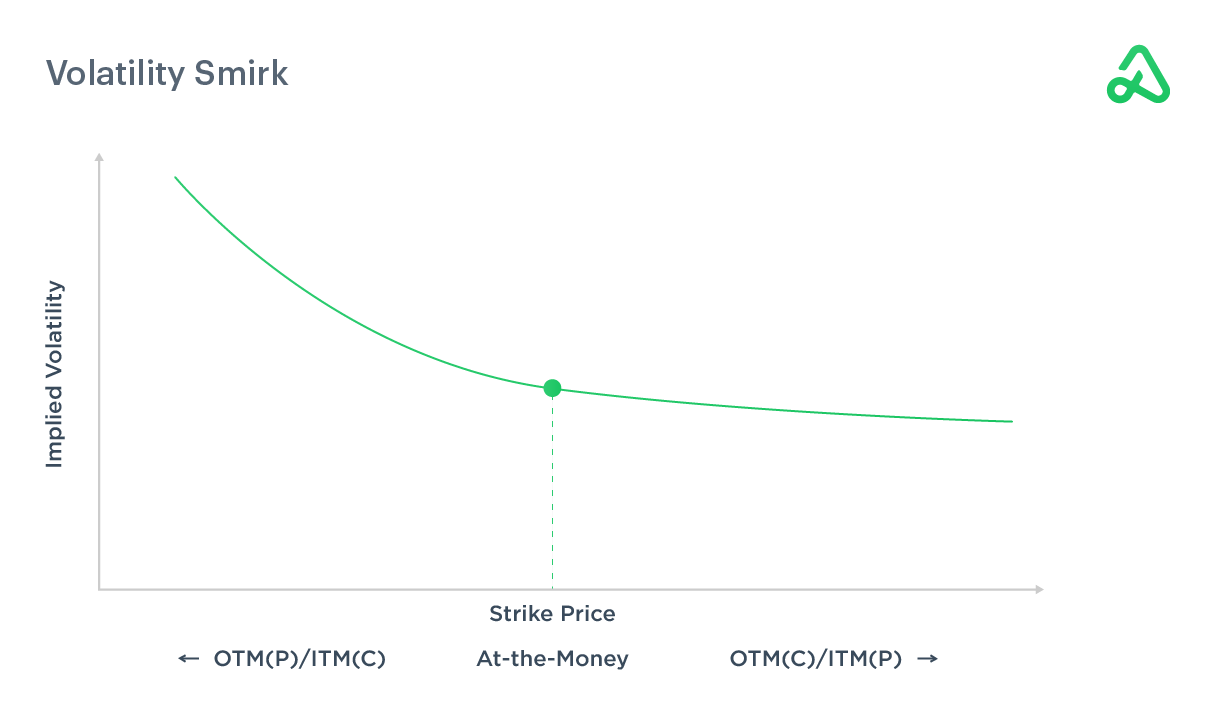
Volatility smile & smirks

Volatility smile refers to the graphical representation plotting implied volatility and an option’s strike price. Implied volatility increases as the strike price is further out-of-the-money or further in-the-money compared to at-the-money.

Because of this increase on either side of at-the-money, the graph of implied volatility and strike price resembles a smile. The graph shows options contracts furthest away from the money have the highest implied volatility. 

Volatility smirk refers to the volatility skew that commonly occurs in options pricing where in-the-money calls and out-of-the-money puts are relatively more expensive compared to out-of-the-money calls and in-the-money puts.

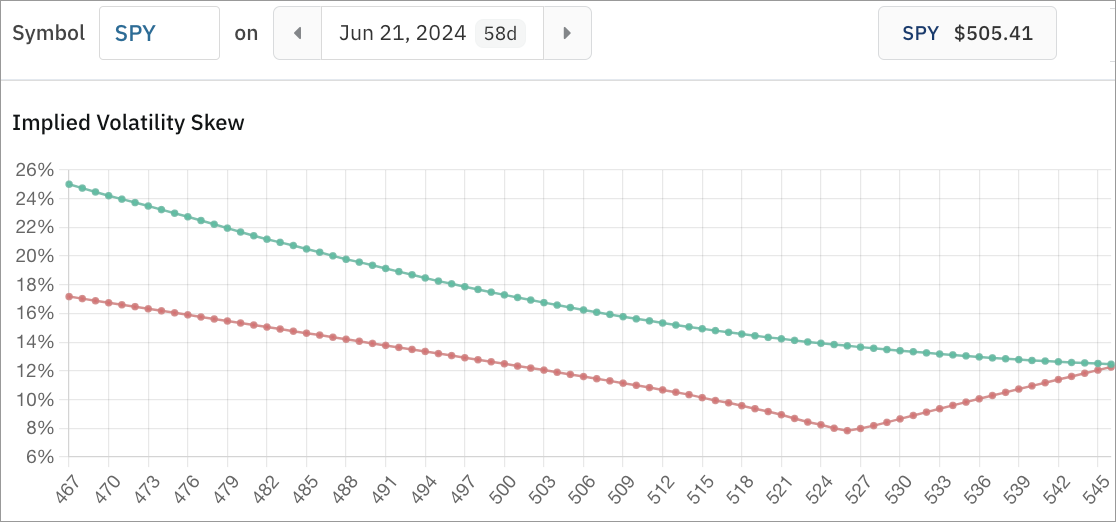
Higher volatility expectations are priced into downside protection, such as deep out-of-the-money put options, than upside protection, such as deep out-of-the-money call options, so the downside protection is “overpriced,” relatively speaking. 

Volatility smirks occur because investors are generally more concerned with market crashes than market rallies. Securities tend to rise slowly or float higher during rallies and drop rapidly during crashes. The value of downside protection during periods of market volatility is greater and creates skew in options pricing.

For example, think of purchasing home insurance in an area prone to hurricanes. The risk is greater; therefore premiums will rise as potentially harmful events become more likely.

Volatility smirks are also impacted by what is known as a synthetic collar strategy, where investors purchase put options for downside protection and sell call options to finance the purchase of the put options. This creates a higher demand for the put options while lowering the price of the call options.

Volatility index (VIX)

The Cboe Volatility Index, or the VIX, was designed by the Chicago Board Options Exchange to measure the 30-day expected volatility of the U.S. stock market. The index is calculated using real-time price quotes on S&P 500 Index SPX call and put options. VIX futures and VIX options contracts provide investors with liquid exposure to various volatility trading strategies and risk management approaches.

The VIX is an important indicator of fear and volatility in the market and tends to be mean-reverting. As more fear and uncertainty enters the market, the VIX increases. Periods of high volatility are typically followed by periods of relative calm as the uncertainty is removed from markets. Therefore, large spikes in the VIX tend to be followed by declines as volatility expectations decrease. 

Dividends

Dividends have a relatively minor effect on options prices. However, dividends do impact options pricing because of the price movement of the underlying security as a result of the dividend payment. Security prices are expected to drop by the value of the dividend amount on the ex-dividend date, so high dividend amounts impact options prices more than low dividends.

Dividend payments tend to lower call option premiums and increase put option premiums. If the underlying security does not pay a dividend, then dividends do not impact the price of options for that security.

Call option sellers should pay particular attention to dividends because if the call option is in-the-money and the dividend amount exceeds the remaining time value of the option, they are at greater risk of early assignment because the option holder (buyer) can exercise his or her right and receive the dividend payment. 

Interest rates

Interest rates have a relatively minor impact on short-term options prices. A 90-day Treasury bill’s current interest rate is used to measure the risk-free rate for many options pricing mathematical models. As interest rates rise, call options prices increase while put options prices decrease.

Interest rates impact the value of security prices through models such as the Capital Asset Pricing Model (CAPM) and therefore impact the value of options contracts at different strike prices. Longer-dated options, or LEAPS, may be affected because interest rates may change over the options contract’s duration. The impact of interest rates on options contracts is called Rho.

Black-Scholes Model

The Black-Scholes Option Pricing Model is a mathematical model for pricing options contracts created by Fisher Black and Myron Scholes. The Black-Scholes Model is also referred to as the Black-Scholes-Merton model for Robert Merton’s contribution to the work. For their work in options pricing theory, Scholes and Merton received the 1997 Nobel Prize in Economics. 

The Black-Scholes Model has five inputs: the current stock price, the option strike price, the risk-free interest rate, the time remaining until expiration, and the underlying security’s volatility. The model assumes a European-style expiration, efficient markets, no dividends, no transaction costs, stable volatility, constant risk-free rate, and the underlying security’s returns are normally distributed. Developments discovered since the model’s creation, such as volatility skew, have introduced additional limitations. Still, the Black-Scholes model revolutionized the options industry and is still widely used today.

Binomial pricing model

The binomial options pricing model uses an iterative, decision-tree approach to determine an options contract’s value. One-period, two-period, and multi-period binomial option pricing models can be used to calculate the value of an options contract across different underlying security prices. The binomial approach is also used in risk management applications for portfolio allocation decisions by determining the appropriate number of call options, put options, and long stock positions under various price scenarios.

Unlike the Black-Scholes Option Pricing Model, binomial pricing models can be used for American-style options contracts and provide insight into whether or not an options contract should be exercised early. Compared to the Black-Scholes Option Pricing Model, many find binomial pricing models more intuitive and are, therefore, more frequently used when pricing options. As more periods are added to the binomial option pricing model, the option price calculated using the binomial model converges on the calculated price of the Black-Scholes model.

Monte Carlo simulation

Monte Carlo simulations estimate solutions or expected outcomes for complex problems by running multiple iterations, or simulations, of variables across expected ranges. Thousands of simulations are run to create a confidence interval, or probability, that the expected outcome lies within a certain range.

Monte Carlo simulations generate random numbers from probability distributions for each variable considered to make reasonable approximations for problems and potential scenarios. Potential distributions include standard-normal, triangular, log-normal, or poisson, along with many others. Monte Carlo simulations are also called multiple probability simulations.

Monte Carlo simulations have multiple finance applications because many independent variables have to be considered simultaneously when investing, such as retirement planning, portfolio construction, risk management, and numerous other areas. This simulation method was originally developed by Stanislaw Ulam and John Von Neumann in 1946 as a method to estimate probabilities in solitaire.

Bjerksund-Stensland model

The Bjerksund‐Stensland Model is a closed-form options pricing model used to value American-style options contracts. The Bjerksund‐Stensland Model is used to estimate the best time to exercise an options contract.

The Bjerksund‐Stensland Model approximates the value of options contracts quicker and more efficiently than other pricing models and is frequently used in brokerage platforms to calculate prices.

Options Greeks

Option Greeks are used to represent the variables that determine an option’s constantly changing price. "The Greeks" reflect how outside factors will impact an option’s value as certain conditions change.

Options prices do not always move equivalently to the underlying asset’s price, and the Greeks help explain why. Greeks do not directly influence options pricing and will not indicate where an asset’s price will trade in the future. Instead, the Greeks are a way to measure an option's sensitivity to ever-changing external factors. Their values are dynamic and will fluctuate as price and information changes.

On most platforms, the Greeks are listed on the options chain along with the bid/ask price, volume, and open interest. 

There are many elements to an option’s price. Time until expiration, implied volatility, changes in the underlying asset’s price, and interest rates all impact the value of an option. There are five main Greeks, and each relates to either the option’s intrinsic or extrinsic value.

Delta and gamma are dependent on the option’s spot and strike price and are therefore derived from intrinsic value. Theta, vega, and rho are determined by time to maturity, volatility, and interest rates, all of which are components of extrinsic value.

Delta

Delta is the amount an options price should change based on a $1 move up in the stock. 

Call options have a positive delta between 0 and 1, while puts have a negative delta between 0 and -1.

Delta would represent the number of relative shares you would own if you purchased an option at a specific delta. Buying a call option with a .50 delta is roughly equivalent to owning 50 shares of stock (and vice versa with put options: -.50 delta is the same as shorting 50 shares).

For example, a stock priced at $100 has a $110 call option expiring in 60 days with a delta of .30 and costs $2.00. If the underlying stock moves up to $101, the option should now be worth $2.30. Owning 100 shares of the stock would have realized a gain of $100. The .30 delta option realized approximately 30 shares worth of value, or $30.

Delta can also act as an approximation of the probability an option will finish in-the-money. A .30 delta has roughly a 30% chance of expiring in-the-money (or a 70% chance of expiring out-of-the-money).

Gamma

Gamma is closely related to delta. Gamma is the rate of change in delta for every $1 change in the underlying price. Gamma represents the acceleration at which an option's price increases or decreases. Think of gamma as the next dollar move. ‍

For example, if an option has a delta of .40 and a gamma of .20, the first dollar move in the underlying asset will see the price of the option change by $0.40 ($40). The subsequent dollar move of the stock will see the price of the option change another $0.40 ($40) plus an additional $0.20 ($20).

Therefore, a $2 move in stock price will result in a total net change of $1.00 ($100) in the option’s price.

Gamma is higher for contracts closer to at-the-money and more sensitive to changes in the underlying asset price.

Gamma risk is the concern that price changes in the underlying asset will have an adverse impact on the option premium. Gamma risk increases as options approach expiration because a small move in the underlying security will significantly impact pricing due to the lack of time remaining on the contract.

Theta

Theta represents the effect time decay has on the value of an option. Options are a decaying asset. Options contracts lose value daily from the passage of time. The rate at which options contracts lose value increases exponentially as options approach expiration. Theta is the amount the price of the option will decrease each day.

For example, a theta value of -.02 means the option will lose $0.02 ($2) per day.

Theta is always represented in negative terms because the portion of an option’s value related to time is always going down. Theta value is smaller further away from expiration and is not constant -- it accelerates more rapidly the closer it gets to expiration.

Theta is an advantage for the option seller and a disadvantage for the option buyer.

Vega

Vega is the amount option prices change for every 1% change in implied volatility in the underlying security. Vega represents an unknown element because future volatility cannot be predicted. All other components of an option’s price can be determined objectively: spot price, strike price, and time to expiration.

Vega has no impact on the intrinsic value of an option. It is not based on price movement in the stock, only changes in volatility.

As volatility increases, an option’s price increases as market participants anticipate an above-average move may be possible before expiration. Vega decreases as it approaches expiration because there is less time for volatility to occur. 

Rho

Rho measures the sensitivity of an option’s price as it relates to changes in interest rates. Rho represents the expected change of a contract’s value for a 1% change in interest rates. Rho is not as important for short-term options traders because changes in interest rates are usually relatively small, and only adjusted once per quarter, if at all.

Long-term options, or LEAPS, are more significantly impacted by changes in interest rates because of their long expiration period. Investors hedging long-term positions with options may also consider rho, as changes in interest rates will affect the value of those positions.