Many factors go into making sound financial decisions. The time value of money (TVM) is one of the most important investment concepts to understand. We’ll explain why, and how you can use it to your advantage when making investment decisions. We'll also provide real-world examples so you can better comprehend its applications.

The time value of money is the concept that money available today is worth more than the same amount of money in the future, because money today can be invested, while money in the future will be worth less due to decreased purchasing power (inflation). Essentially, a dollar today can earn a return, while a dollar tomorrow cannot.

This concept is important to understand because it can significantly impact your investment decisions. For example, when deciding whether to invest in a stock or bond, you'll need to consider the time value of money when making your decision. 

Further, you can think of the interest earned like lending your funds. You should be compensated for putting off purchasing decisions today so somebody else can use those funds. The time value of money explains the return you receive for investing instead of consuming.

Time value of money basics

Here are the key concepts you should know:

Present Value

The present value of a future series of payments is the value today of those payments, taking into account the time value of money. In other words, it is the amount you would need to invest today at a certain rate for a certain period of time to have a certain amount of money in the future.

Future Value

The future value of a series of payments is the value of those payments at a future date, taking into account the time value of money. In other words, it is the amount you will have in the future if you invest a certain amount of money today at a certain rate for a certain period of time.

Discount Rate

The discount rate is the interest rate used to discount a series of payments back to their present value. The terms growth rate, discount rate, and required rate of return are often used interchangeably when discussing the TVM.

Present Value of an Annuity

An annuity is a stream of equal payments made at regular intervals. The present value of an annuity is today's value of a stream of future payments, taking into account the time value of money.

Future Value of an Annuity

The future value of an annuity is the value of a stream of future payments at a future date, taking into account the time value of money.

Present Value of a Perpetuity

A perpetuity is a stream of equal payments made at regular intervals that continues indefinitely into the future. The present value of a perpetuity is today's value of the stream of payments, taking into account the time value of money.

Future Value of a Perpetuity

The future value of a perpetuity is the future value today of a stream of payments that continues indefinitely, taking into account the time value of money.

Discounted Cash Flow (DCF) Analysis

Discounted cash flow analysis is a method of valuing a project or company by discounting its cash flows to present value.

Net Present Value (NPV)

The net present value of a project is the present value of its cash flows minus the initial investment.

Internal Rate of Return (IRR)

The internal rate of return is the discount rate that makes the NPV of a project equal to zero

Payback period

The payback period is the time it takes for the NPV of a project to equal the initial investment. The payback period does not take into account the time value of money.

How does the time value of money work?

To understand how the time value of money works, let's look at an example. 

Suppose you have $100 that you want to invest. You can either invest it now, or you can wait a year to invest. If you invest the $100 now, it will grow at a rate of return (r). After one year, your investment will be worth:

$100 * [1 + r]

If your rate of return is 10%, your investment will be worth $110 after one year. Some formulas use i (interest) instead of r (return), but both refer to the same variable. 

Investing your money sooner rather than later is always advantageous because the time value of money generates returns that uninvested capital does not.

Calculating the present and future value of money

The time value of money can be calculated using a simple equation. The equation is:

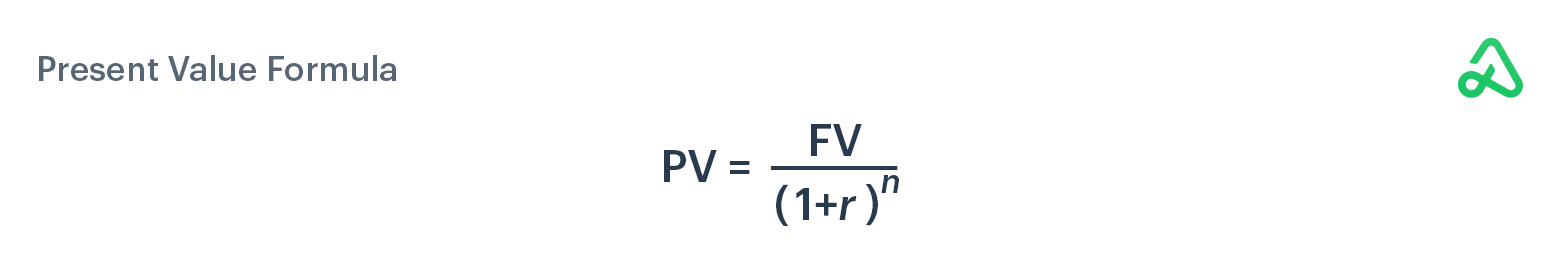
Where:

• PV = present value
• FV = future value
• r = rate of return
• n = number of years

For example, let's say you want to have $100 in 10 years. If your rate of return is 10%, the present value of your investment would be:

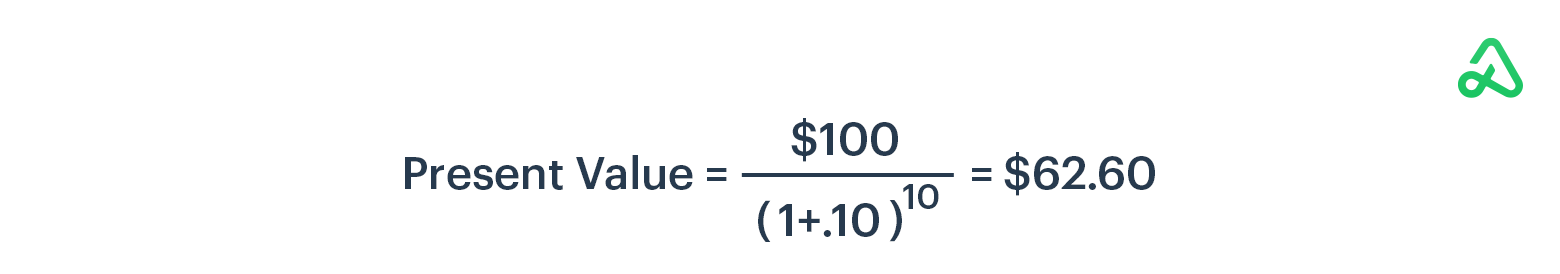
If you invest $62.60 now at 10%, it will be worth $100 in 10 years.

You can also use this equation to calculate the future value of money. Rearranging the equation from above gives you:

For example, assume you have $100 that you want to invest for 10 years. If your rate of return is 10%, the future value of your investment would be:

If you invest your money now, it will be worth $259.37 in 10 years.

TVM can have a significant impact on your investment decisions. For example, if you are trying to decide whether to invest in a stock or a bond, you can use TVM to compare the variables.

If you are investing for the long-term, you may be better off investing in a stock because it has the potential to earn a higher return than a bond. However, if you need the money sooner, you may be better off investing in a bond because it is less risky and more likely to provide a return of your principal investment.

Time value of money is also essential to understand when considering different investments. For example, let's say you are trying to decide between investing in a stock that pays a dividend or a stock that does not pay a dividend.

TVM suggests that the stock  dividend-paying stock is a better investment because you are receiving payments now rather than in the future. However, the stock that does not pay a dividend may be a better investment if it is expected to grow at a higher rate than the stock that pays a dividend.

It is also important to keep in mind that the time value of money is only one factor to consider when making investment decisions. Other factors such as risk, return, and taxes should also be considered.

The importance of saving money and investing for the future

Compounded interest is often called the "eighth wonder of the world" because compounding is so powerful.

For example, if you have $100 that you want to invest for 10 years and the rate of return is 10%, the future value of your investment would be:

If you invest your money now, it will be worth $259.37 in 10 years. However, if you wait 5 years to invest the $100, it will only be worth:

This shows the importance of saving money and investing for the future as soon as possible. The earlier you start, the more time your money has to grow.

The power of compounding can also be used to your advantage when it comes to debt. For example, let's say you have a $1,000 credit card balance that you want to pay off. The minimum monthly payment is $20 and the interest rate on the credit card is 10%. 

If you make the minimum payment of $20 per month, it will take you 65 months to pay off the debt. However, paying just $5 more, $25 per month, will only take 49 months to pay off the debt. Even a small increase in your monthly payment can save you significant money in interest payments.

The time value of money is an important concept that can help you make better decisions about saving, investing, and managing debt.