Efficient market hypothesis
The efficient market hypothesis is a financial theory built on the assumption that stock prices reflect all information available in the market, and the current price of an asset is an expression of its true value. Therefore, supporters of the efficient market hypothesis believe that it is not possible to find value in the stock market because all assets are priced exactly as they should be.
The efficient market hypothesis has three forms: weak-form efficient markets, semi-strong form efficient markets, and strong-form efficient markets. Each category is dependent on the availability of information to test the idea that all information is known.
The weak-form states past price information is unrelated to future price action, so historical price data (technical analysis) does not yield an advantage.
The semi-strong form states prices currently reflect all public information such as financial statements, so fundamental analysis should not yield an advantage because prices rapidly respond to new information as released.
The strong-form states all information, both public and private, is priced into markets.

The efficient market hypothesis is widely debated in the finance community. Many believe in some level of weak and semi-strong efficiency, but not the strong form.
However, there are entire industry groups devoted to finding value through fundamental analysis or technical analysis. Those who believe in the theory argue there is no way to exploit market inefficiencies, as they believe there are none.
The hypothesis states that all known variables are automatically factored into an asset’s price by the collective trading in the marketplace and its participants. Because there is no way to find value in asset prices, it is believed to be impossible to outperform the market. Technical or fundamental analysis provides no edge, and investors must take on disproportionate risk, or have access to inside information, to achieve consistent returns.
Opponents of the efficient market hypothesis believe that numerous variables can not possibly be included in the current market price of an asset, and stocks are subject to random movement in price as the result of unknown information or unexpected trading activity. Detractors argue that stocks consistently trade above or below their true market value and can, therefore, be exploited to make money.
Efficient frontier
The Efficient Frontier, introduced by Harry Markowitz in 1952, is a portfolio theory that rates investments in terms of return relative to risk.
Markowitz’s efficient frontier is the basis for modern portfolio theory. The Efficient Portfolio Frontier rates portfolios on a graph where the x-axis is risk as measured by portfolio standard deviation, and the y-axis is the return as measured by the portfolio’s expected return.
The goal is to create the most efficient portfolio construction that optimizes the highest possible return for its level of risk. Portfolios that lie below the efficient frontier on the graph have too much volatility relative to return because there are other combinations of portfolios with a higher expected return for the same volatility or risk level.
Portfolios above the efficient frontier have relatively high expected returns compared to the portfolio’s standard deviation.
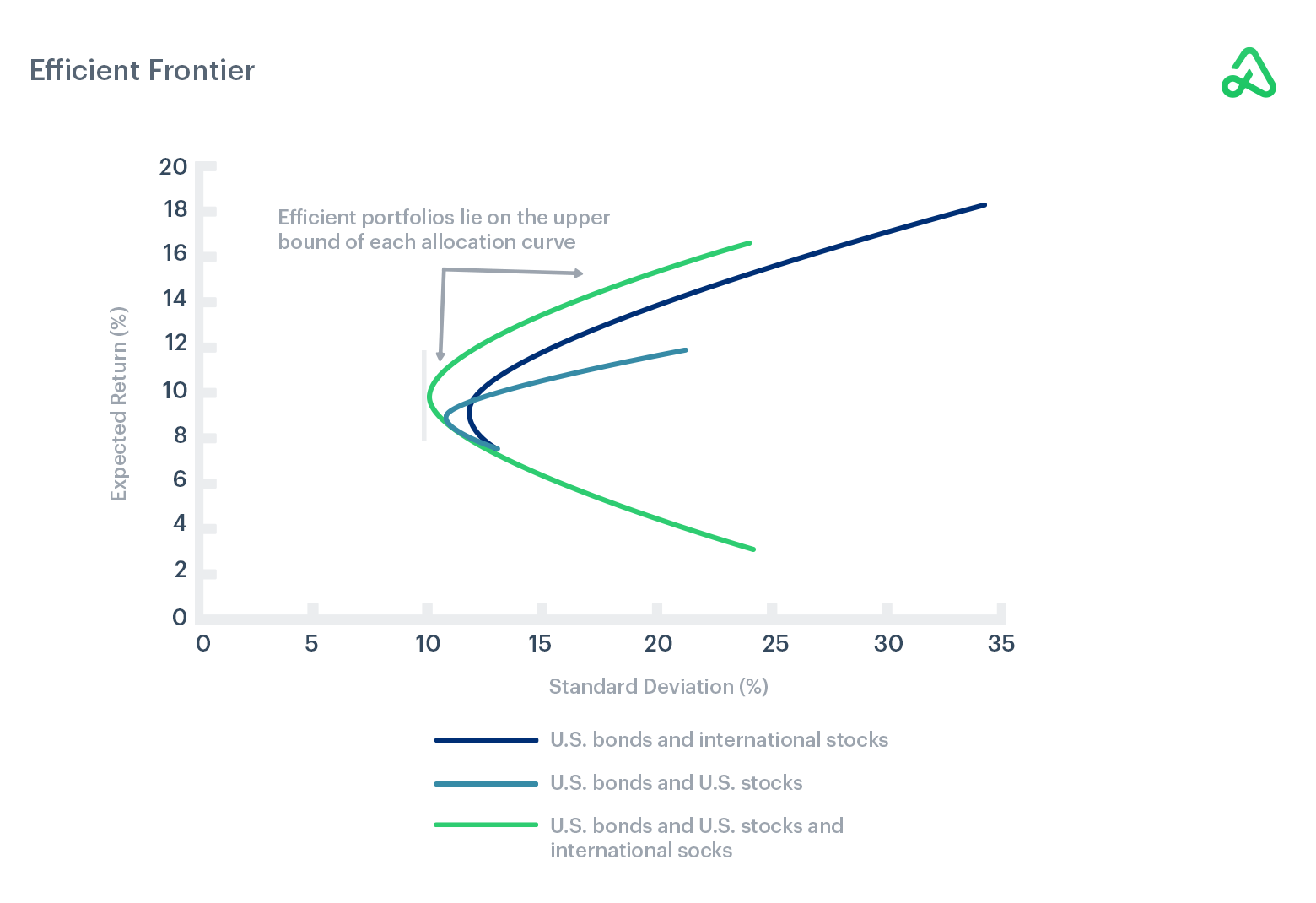
The Efficient Portfolio Frontier takes every possible combination of portfolio asset configuration and plots their risk versus return. It does not seek to find the lowest risk possible or the highest return possible; instead, the goal is to identify the highest expected return for a given unit of risk. The theory states that there is a single ideal portfolio composite for each level of risk or return desired.
Combinations of the risk-free rate, domestic equities, international equities, and other asset classes are considered to determine the optimal portfolio composition for a given level of risk.
Systematic and unsystematic risk
Risk is inherent in all forms of investing. Total risk consists of systematic risk and unsystematic risk.
Systematic risk refers to the risk that affects almost all assets in the economy. Systematic risk is unavoidable and unpredictable. Unsystematic risk is limited to risks associated with trading a specific security or asset class and can be mitigated through hedging or diversification.
Systematic risk
Systematic risk is unavoidable and is often referred to as market risk because it is influenced by macro events that would subsequently impact every form of investing.
Systematic risks include uncertainties surrounding GDP, interest rates, inflation, and black swan events such as natural disasters.
Therefore, any investment in the market is susceptible to systematic risk. If a portfolio is well balanced, there is potential for one asset class to prosper while another struggles. However, systematic risk can never be completely eliminated, as the entire market would likely be affected.
Unsystematic risk
Unsystematic risk is the inherent risk of investing in one specific asset or sector. Unsystematic risk comprises unanticipated events that would only impact a company or small subset of the market, unlike a large scale event like a sudden market crash.
Unlike systematic risk, unsystematic risk can be greatly reduced through diversification to eliminate the consequences of an individual stock price decline. For example, if a portfolio is balanced and diversified, and a stock declined because of the company’s bad earnings, the rest of the assets should not be affected by the issues of one specific company. Unsystematic risk may be significantly reduced through diversification, so that systematic risk is all that remains in a portfolio.
Security market line
The security market line describes the relationship between systematic risk and expected returns by plotting the expected return for a security relative to its systematic risk in the market.
Beta represents a security’s systematic risk. Beta is a value that describes a stock’s volatility compared to the overall market. A beta of 1 is considered to have average, or market-like, risk and will typically move up and down in conjunction with the market. A beta higher than one is indicative of more volatility than the market and is, therefore, riskier, but should be expected to produce a higher return.
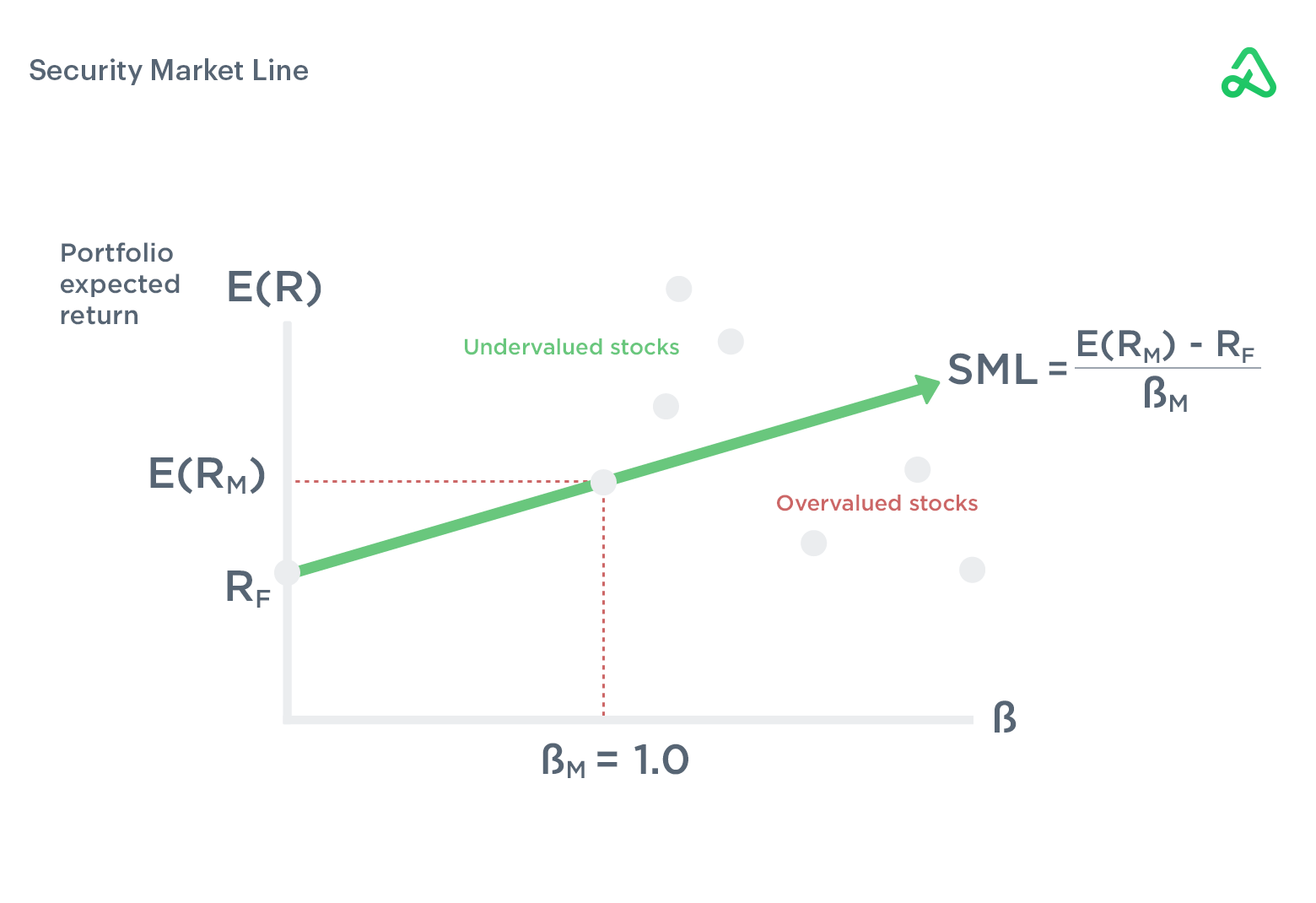
The Security Market Line is visually represented on a graph as sloping up and to the right. The beta for a stock is on the x-axis, while the expected return is on the y-axis. The Security Market Line is a visual representation of the Capital Asset Pricing Model (CAPM).
The expected return for the security is a combination of the risk-free rate, the market risk premium, and the stock’s beta. The expected return of the market minus the risk-free rate is the market risk premium. The expected return for the security is the risk-free rate plus the market risk premium times the stock’s beta.
All assets should plot along the security market line in an efficient market. As expected return increases, the beta should increase, keeping the reward-to-risk ratio the same for all stocks.
Assets above the SML are undervalued compared to their risk, as their rate of return is higher than expected. Assets below the line are overvalued and are not adequately compensated for the risk and capital allocation required to hold the position over time.
Capital asset pricing model (CAPM)
The capital asset pricing model (CAPM) is used to determine a risky asset’s expected return based on the time value, the market risk premium, and the asset’s beta.
The CAPM is used to determine if an asset is fairly valued relative to its expected rate of return. The CAPM prices assets based on their expected returns compared to the risk required to generate the returns, along with the cost of capital as it pertains to the time value of an investment.
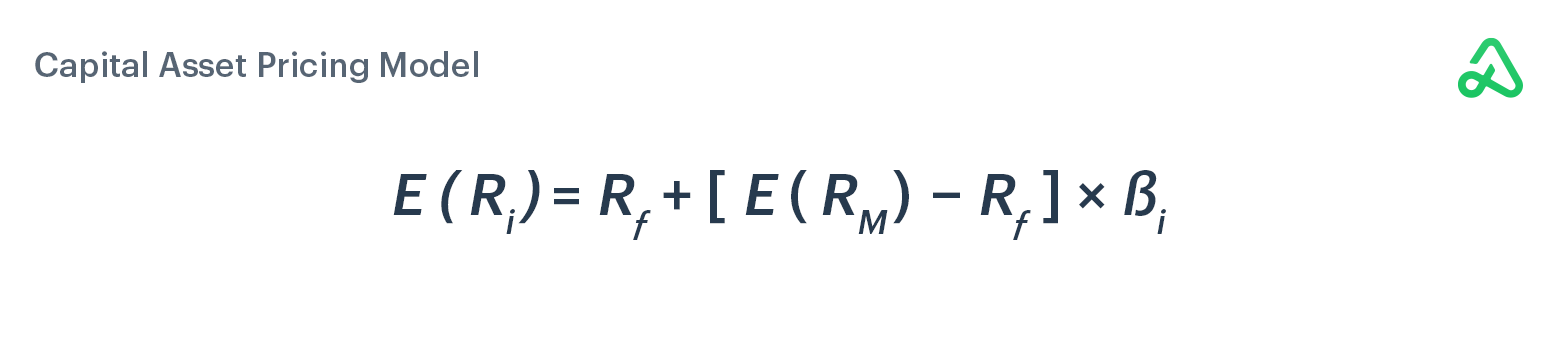
The capital asset pricing model calculates the value of an asset based on the risk-free rate plus the market risk premium times the security’s beta. The market risk premium is equal to the expected return of the market minus the risk-free rate. The risk-free rate refers to the theoretical amount an investment would yield with zero risk. 3-month Treasury bills are typically used as the input for the risk-free rate.
While no truly riskless security exists, as all investments are subject to systematic risk, Treasury bills are the best approximation of a riskless security. The risk-free rate helps account for opportunity cost, or the time value of money, when it is allocated to a specific asset.
There are flaws associated with CAPM, as it relies on assumptions and estimates for the market’s expected return. But it is still widely used as a tool to determine if asset prices are fairly valued and is used in conjunction with the Efficient Frontier and Capital Market Line.
Many still believe the capital asset pricing model is one of the best ways to evaluate an asset’s expected return relative to its market risk.
Random walk hypothesis
As the name suggests, the random walk hypothesis builds its foundation on the principle that markets are random, and prices move independently from one another and their past performance. Therefore, any attempt to predict an asset’s future price, either through technical or fundamental analysis, is impossible.
The random walk hypothesis has been popularized in a number of influential books, and its supporters advocate passive investment in lieu of stock-picking.
The random walk hypothesis aligns with the weak-form of the efficient market hypothesis and believes that all stock price movement is purely random because all information readily available is represented in an asset’s current market value.
Under the weak-form, historical market prices should not be useful in predicting future returns. Therefore, instead of trying to find value in the market, investors are better off passively investing in diversified portfolios because the only way to outperform the market is to get lucky or take on outsized risk.
Black swan
The black swan theory, or theory of black swans, refers to surprise events with significant impact, often beyond the expectations of standard forecasting models and risk management guidelines. The theory was popularized by Nassim Taleb in 2007, just before the financial crisis.
Black swans are extremely rare events that cannot be predicted, and their impact is often multiple standard-deviations beyond expectations. Black swan events can have catastrophic effects on financial markets.
Diversification and balanced portfolios may help offset a black swan’s damage, but, by their nature, the unforeseeable event will most likely disrupt all asset classes simultaneously through correlation.
Black swan events are economic anomalies that can neither be predicted nor fully mitigated. Models and theories have been created to anticipate potential disruptions but have only succeeded in highlighting the unpredictable nature of black swan events.
Many have tried to identify causes in retrospect but have difficulty extrapolating the findings to prevent future black swans. The main reason these attempts fail is the fact that black swan events rarely mirror one another. Each is unique in its own way.
For example, the stock market crash in 2020, as a result of the COVID-19 pandemic, could not be predicted, and the effect it had on global economies was disastrous.
Black swans highlight the inefficiency of predictive models and asset pricing pertaining to unpredictable events, especially the “tail risk” associated with outlier events.
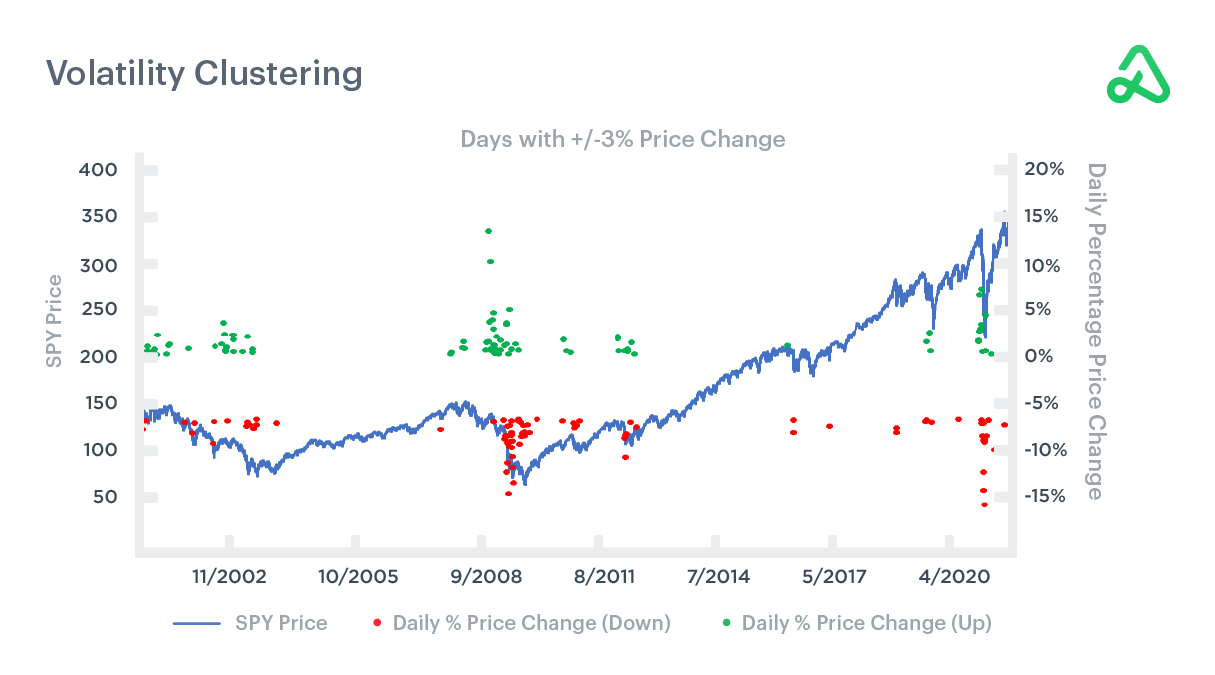
Volatility clustering
Volatility clustering is the propensity for large movements in security prices to group together and promote similarly volatile moves in the immediate future. In financial markets, a sudden increase in volatility tends to be followed by extended periods of high volatility and is subsequently followed by extended periods of low volatility.
Research has found that volatility in an asset or market typically remains high for an extended period of time. After an initial unexpected spike in volatility, it is not uncommon that the volatile conditions will remain in the market for a sustained duration before eventually returning to prolonged conditions of low volatility.
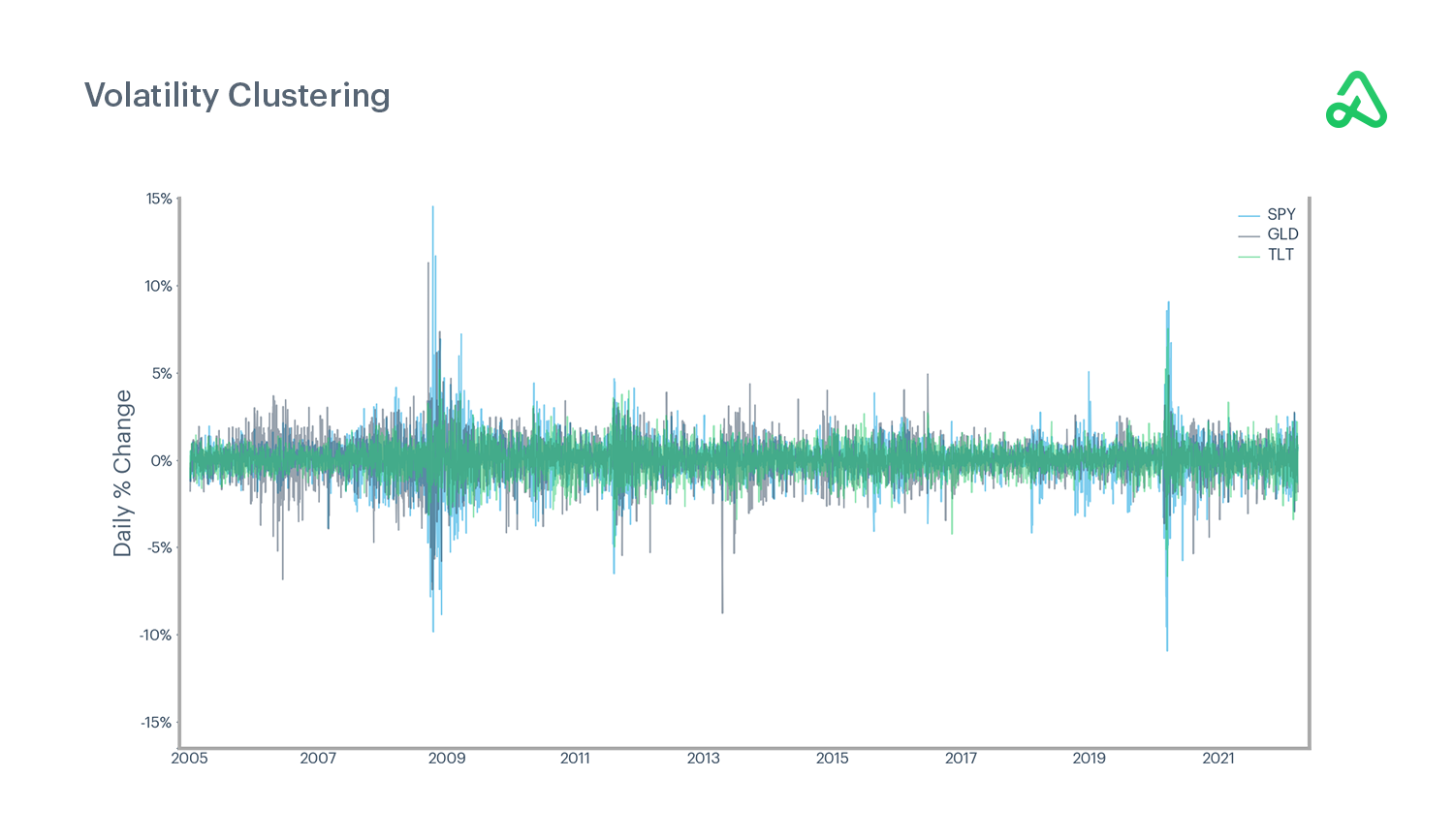
Volatility clustering demonstrates the widespread effect of volatility spikes, as previously uncorrelated assets become correlated and offset attempts to diversify a portfolio.
During periods of low volatility, assets are often loosely correlated and give no indication for impending spikes in volatility. Securities tend to move independently of one another, which may lead to a false belief that diversification is sufficient to mitigate losses when volatility rises.
However, when volatility increases, securities autocorrelate, and assets with little or no previous correlation suddenly move in sync with one another, thus rendering diversification relatively ineffective when markets crash.
The chart below illustrates how previously uncorrelated securities experienced volatile price changes simultaneously when market volatility increased. As the market endured bouts of extreme volatility, assets began moving together, reducing or eliminating the benefits of diversification on previously uncorrelated assets when volatility develops.
Volatility clustering works in opposition to the random walk hypothesis because volatility clustering suggests a historical pattern can be observed.
One model for testing volatility clustering is autoregressive conditional heteroskedasticity (ARCH). ARCH demonstrates that volatility clustering can be thought of as mean-reverting after the prolonged spikes in volatility.
Periods of significant price changes are typically replaced by periods of steady, less volatile price action. Months and years of low volatility in markets can suddenly be disrupted by extreme volatility. Large moves--up and down--cluster into relatively short periods of high volatility, only to be followed by extended periods of low volatility.
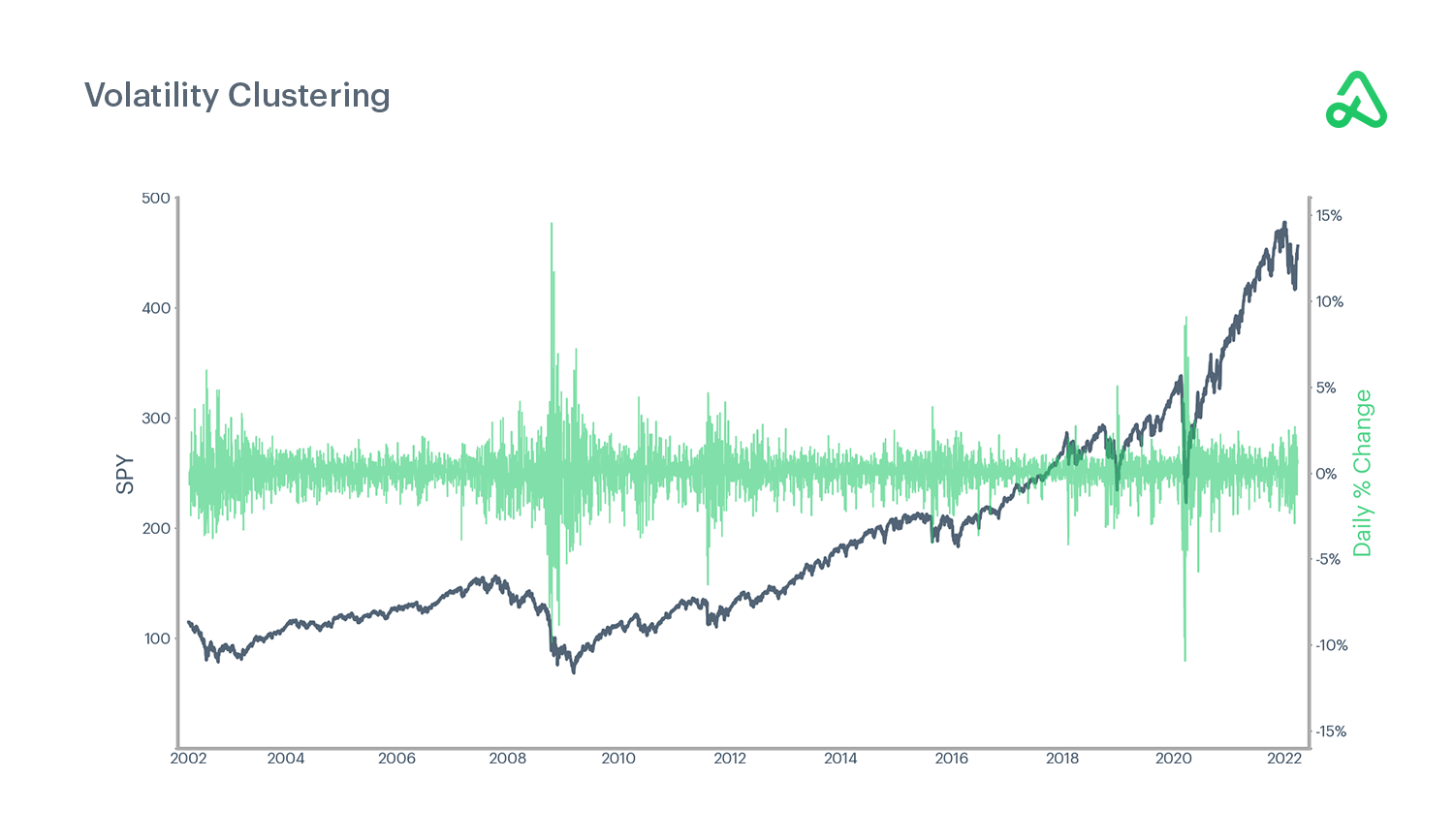
The chart below illustrates how high and low volatility clusters together and is subsequently followed by reversion to the preceding market condition. The chart depicts 20 years of the broad-market ETF, SPY.
From 2000 through 2020, SPY often went prolonged periods with no daily price changes of +/-3%. SPY experienced almost no days with +/- 3% price change in a single day from 2003-2008. However, once volatility entered the market, it was a constant presence until late in 2011, when the market returned to many years of low volatility. What is interesting to note is that not all volatility is to the downside. There are nearly equal amounts of days with ≥ 3% daily price change as ≤ 3% daily price change during the volatile periods.